Using Binary Search to solve optimization problems

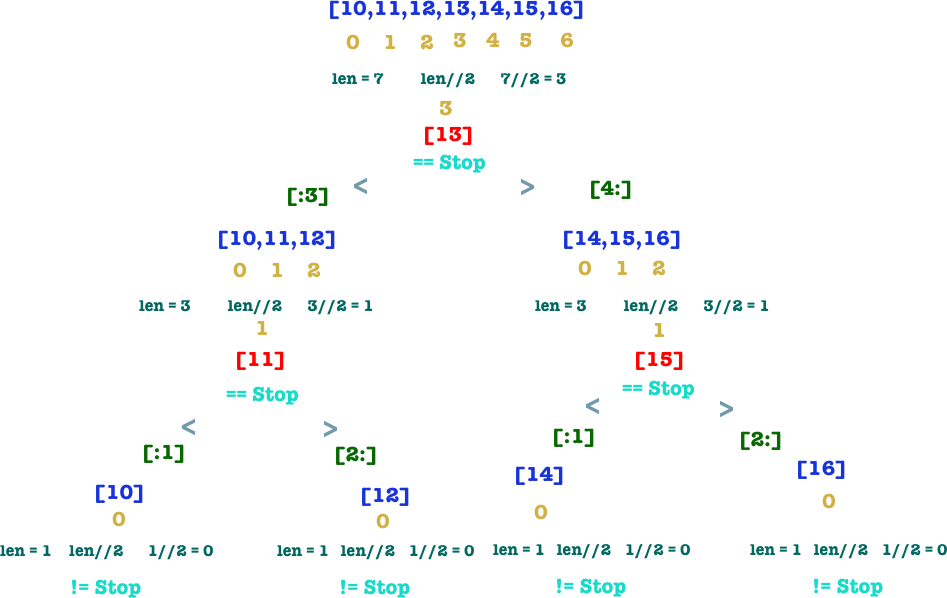
Binary Search, is one of the first algorithms taught to computer science students. It is a simple, divide and conquer algorithm, which can be implemented iteratively or recursively without much trouble. The simplicity and efficacy of binary search serves as a prime example of how a carefully chosen algorithm can make a big impact on the performance of the application. The following points define binary search accurately:

Binary Search:

1. Is a Divide and Conquer algorithm
2. Runs in O(log n)
3. Requires array to be sorted

Below is the implementation of binary search in Python.

Going beyond the traditional binary search: Binary search based optimization for monotones

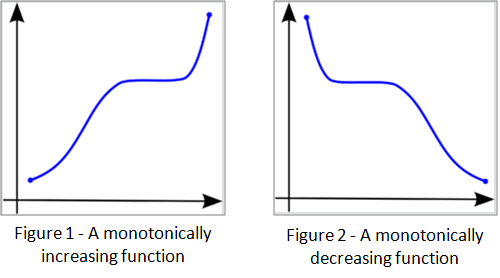
Monotonic functions are functions that are constantly increasing or constantly decreasing throughout the domain of the function. Often in algorithms, we are required to find a optimal point in this monotonic function (which has a huge domain, ruling out brute force). In such cases, binary search comes to our rescue.

The idea of finding the optimal point in the domain of a monotone is similar to the traditional binary search, only this time, instead of an array, we have the following:

• Monotonic function
• Domain of monotonic function
• A condition (usually with a threshold value) that tells what output is acceptable and what is not

So, given this, lets look at the psuedocode for bsearching accross a monotonic function.

# f is monotone
ans = inf # -inf if searching for maximal value
lo = domain_low, hi = domain_high
while lo <= hi:
   mid = (lo + hi)/2
   val = f(mid)
   check val with threshold:
   if admissible:
    update ans if val is better
    discard the half of domain space that is useless
   else:
    discard the other half

Let's have a look the code in detail.

Putting it together: Solving SPOJ's aggressive cows problem

Link to the problem: SPOJ Aggressive Cows

It is recommended that before reading the content below, keeping the idea that we discussed above, give the problem a go.

Solution:

1. In this problem, c is the threshold.
2. A gap variable, which tells the minimum admissible distance between the cows for the given iteration of computation. Our goal is to find the minimal gap value, such that acceptable cows >= c
3. Monotonic function. Let f(x,arr) be the function that counts the number of acceptable cows(cows that are atleast x units apart) in the sorted array.
   If we have k acceptable cows in the array that are atleast x units apart from each other, you will, by nature have atleast k acceptable cows that are x-1 units apart.
   In other words, f(x,arr) <= f(x-1,arr) always holds. Thus, we can argue that f(x) is strictly a monotonically decreasing function.
4. Run binary search over this function to find the optimal x

Code:

Conclusion

Binary search can often be used for problems that involve finding the optimal point, on a monotonic function. The running complexity of O(log n), without any additional space requirement, and its nature of being simple to implement makes binary search a frequently used algorithm in such situations.

Well then, until next time!